Im vom Bundesministerium für Bildung und Forschung (BMBF) geförderten Projekt „SKILL“ (Strategien zur Kompetenzentwicklung: Innovative Lehr- und Beratungskonzepte in der Lehrerbildung) an der Universität Passau entstehen neue vernetzte Lehr-Lern-Formate für eine innovative Lehrerbildung. Das Teilprojekt Mathematik entwickelt dabei eine „interaktive mathematische Landkarte“, mit deren Hilfe sich die Studierenden in einem Seminar die Zusammenhänge zwischen Schul- und Hochschulgeometrie verdeutlichen können. Dadurch soll die Relevanz des fachwissenschaftlichen Studiums für den späteren Lehrberuf deutlicher hervortreten.
Montag, 8:15 Uhr Mathematikvorlesung: 90 Minuten hohes Niveau, das volle Konzentration erfordert. Jede Definition muss schnell verinnerlicht werden, da sie für die darauf folgenden Sätze benötigt wird. Ebenso werden die meisten Sätze und Lemmata im Beweis des nächsten Satzes oder Lemmas benutzt. Diesen, teils mehrseitigen Beweisen Schritt für Schritt zu folgen, erfordert einige Anstrengung. Am Ende der Vorlesung verlassen die Studierenden den Hörsaal ziemlich erschöpft und voller Fragen: „Wozu brauche ich das denn bitte?“ – „Wieso muss ein Lehrer sowas wissen?“ – „Das hat doch nichts mit dem Schulstoff zu tun!“
Diese oder ähnliche Vorwürfe muss sich die universitäre Mathematikausbildung für Lehramtsstudierende immer wieder gefallen lassen. Viele Studierende sehen keinen Sinn in der fachwissenschaftlichen Ausbildung, da sie die Schulmathematik (das, was von ihnen gelehrt werden soll) und die Hochschulmathematik (das, was sie gerade lernen sollen) als zwei getrennte Welten wahrnehmen. Sie übersehen, dass sie durch die Betrachtung des Stoffes aus einer höheren Warte ein tieferes Verständnis erzielen und dadurch im späteren Unterricht verständlichere und fachlich besser fundierte Erklärungen geben können.
Aber das ist keineswegs ein Phänomen unserer Zeit. Schon der berühmte Mathematiker Felix Klein schrieb 1908:
„Der junge Student sieht sich am Beginn seines Studiums vor Probleme gestellt, die ihn in keinem Punkte mehr an die Dinge erinnern, mit denen er sich auf der Schule beschäftigt hat; natürlich vergißt er daher alle diese Sachen rasch und gründlich. Tritt er aber nach Absolvierung des Studiums ins Lehramt über, so soll er plötzlich eben diese herkömmliche Elementarmathematik schulmäßig unterrichten; da er diese Aufgabe kaum selbstständig mit der Hochschulmathematik in Zusammenhang bringen kann, so wird er in den meisten Fällen recht bald die althergebrachte Unterrichtstradition aufnehmen.“ (Elementarmathematik vom Höheren Standpunkte aus, S.1)
Hier muss also Veränderung her! Einen ersten, fächerübergreifenden Schritt geht dazu das vom Bundesministerium für Bildung und Forschung (BMBF) geförderte Projekt SKILL. Es hat zum Ziel, die Fachdisziplinen und Fachdidaktiken in der Lehramtsausbildung besser zu vernetzen und die Lehramtsausbildung insgesamt stärker in den Fokus zu rücken. Dabei werden im Teilprojekt Mathematik – nach der Idee des Passauer Mathematikdidaktikers Prof. Dr. Matthias Brandl – sogenannte „interaktive mathematische Landkarten“ erstellt.
Eine interaktive mathematische Landkarte sieht aus wie ein virtueller dreidimensionaler Baum bzw. ein Netz. Die einzelnen Verzweigungsstellen bzw. Knoten stellen dabei wichtige Entwicklungen in der Mathematik dar und sind mit anderen Knoten verbunden, die auf diesen Entwicklungen beruhen. Dabei wird in der horizontalen Dimension die thematische Nähe zweier Knoten durch ihren Abstand dargestellt und in der vertikalen Dimension die zeitliche Entwicklung (Abb. 1).
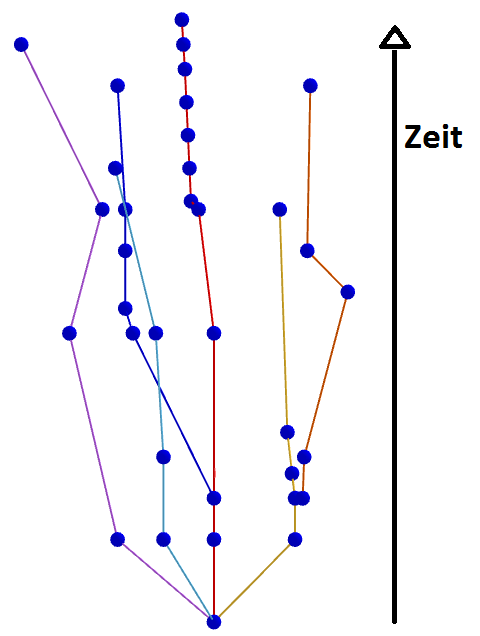
Wenn man sich zum Beispiel den Ausschnitt über die Satzgruppe des Pythagoras und dazu verwandte Themen anschaut, sieht das schematisch gesehen wie folgt aus:
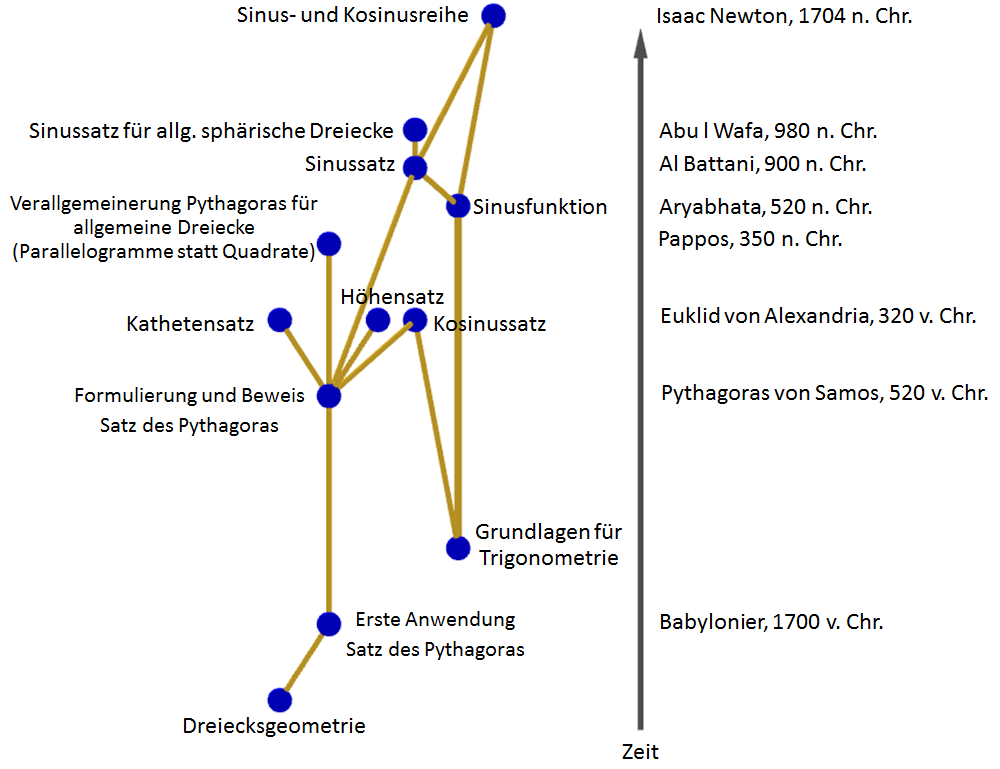
Die Satzgruppe des Pythagoras gehört zur Dreiecksgeometrie – hier beginnt der Baum. Erstmalig wird die Formel „a2 + b2 = c2“ 1700 v. Chr. auf einer Tontafel in Babylon erwähnt. Die Formulierung und der Beweis des Satzes geht zurück auf den Namensgeber, Pythagoras von Samos (520 v. Chr.) – der nächste größere Abschnitt im Baum. Aus dem Satz des Pythagoras lassen sich direkt der Höhensatz und der Kathetensatz ableiten. Diese wurden in den Elementen von Euklid (320 v. Chr.) bewiesen. Der Sinussatz und der Kosinussatz hängen auch eng mit dem Satz des Pythagoras zusammen, jedoch benötigt man dafür noch trigonometrische Funktionen. Soweit wird noch alles in der Schule behandelt. Aber die Mathematik hört hier noch nicht auf. Der Satz des Pythagoras lässt sich in abgewandelter Form auch auf beliebige Dreiecke anwenden. Dabei ersetzen Parallelogramme die Quadrate im Satz des Pythagoras. Man erhält dann die Flächenformel von Pappos (350 n. Chr.). Ebenso lässt sich der Sinussatz erweitern auf allgemeine sphärische Dreiecke (Abu l Wafa, 980 n. Chr.). Die Sinus – und die Kosinusfunktion besitzen auch eine Reihendarstellung. Diese wurde zuerst von Isaac Newton gefunden (1704 n. Chr.). Zu all diesen – teils deutlich über die Schulmathematik hinausgehenden – Themen können weitere Informationen online zur Verfügung gestellt und an den einzelnen Knoten verlinkt werden.
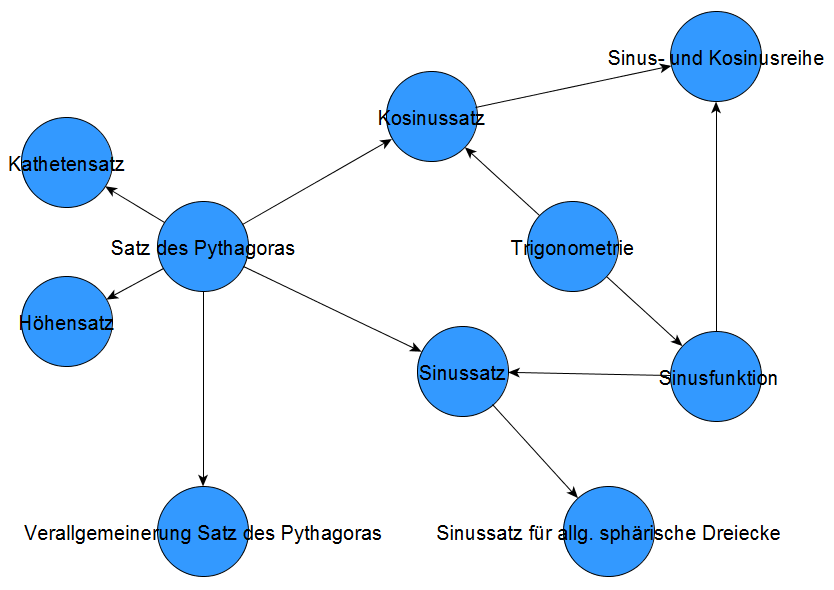
Die Stärken einer solchen interaktiven mathematischen Landkarte liegen darin, dass durch die Visualisierung in drei Dimensionen die Zusammenhänge besser nachvollzogen werden können. Anhand von Abbildung 2 sieht man den Vorteil gegenüber einer Darstellung in nur zwei Dimensionen: Die Anordnung lässt vermuten, dass zwischen dem Höhensatz und dem Kosinussatz eine enge thematische Verwandtschaft besteht – scheinbar enger als zwischen Höhensatz und Kathetensatz. Tatsächlich ist das aber nicht der Fall: Der täuschende Eindruck der thematischen Nähe kommt dadurch zustande, dass in Abbildung 2 die dritte Dimension, die aus der Skizze heraus, bzw. in die Skizze hinein geht, nicht dargestellt werden kann. Der Grafik fehlt also der interaktive Aspekt der interaktiven mathematischen Landkarte. Dieser erlaubt es unter anderem, dass die Landkarte gedreht werden kann und thematische Verwandtschaften besser dargestellt werden können.
In der fertigen interaktiven mathematischen Landkarte werden am Ende die Beziehungen zwischen den einzelnen Knotenpunkten also noch besser erkennbar sein. Das ist für das Lehren und Lernen eine enorme Erleichterung. Ein weiterer Vorteil dieser Visualisierung ist, dass die Entwicklung eines Themas im Zeitverlauf verfolgt werden kann (der Zeitpfeil neben den Knoten). Ebenso kann man sich in der Landkarte sogenannte horizontale Schnitte anzeigen lassen. Diese bilden den momentanen Entwicklungsstand und die thematische Nähe verschiedener Themenbereiche zu einem bestimmten Zeitpunkt ab (Abb. 3). Zusätzlich können die einzelnen Knoten mit weiterführenden Informationen im Netz oder zusätzlichen Materialien verlinkt werden, die z.B. auf einer Lernplattform wie ILIAS oder Moodle hinterlegt sind.
Solche interaktiven mathematischen Landkarten können dann in Seminaren eingesetzt werden. Eine Testphase für den Bereich der Geometrie ist am Lehrstuhl von Prof. Dr. Brandl im Wintersemester 2017/2018 geplant. Die Vorteile der dreidimensionalen Visualisierung werden es den Studierenden erleichtern, die Zusammenhänge zwischen Schul- und Hochschulmathematik zu verstehen.
Die interaktiven mathematischen Landkarten werden die Studierenden auch dabei unterstützen können, sich eigene Beispiele zu Theorien zu überlegen und diese für den späteren Schulunterricht als Lehr- und Lernmaterial einzusetzen. Zu hoffen ist, dass künftige Generationen von Studierenden, aber auch von Schülerinnen und Schülern, sich dadurch besser im vermeintlichen Irrgarten der mathematischen Theorie orientieren können – und dabei Spaß haben.
Geometrie_in_Schule_und_Hochschule_SeminardokumentationAlle Abbildungen: © Andreas Datzmann 2017 (mit GeoGebra/ yEd Graph Editor)
Andreas Datzmann war Wissenschaftlicher Mitarbeiter im Projekt SKILL in der Lehr- und Forschungseinheit "Lehramtsausbildung und Mathematik" (LMI).
